2019-09-27

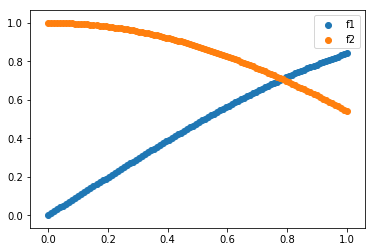
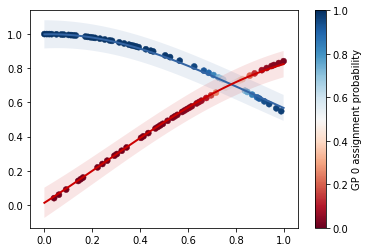
混合ガウス過程で多峰な関数を回帰する

機械学習系技術系

忘備録として

混合ガウス過程と多峰な関数

以下のような多峰な関数を回帰する場合は，通常の単峰にフィッティングする回帰では困難なので混合ガウス過程を用いる．

f:id:suzuzusu:20190927182219p:plain — f1，f2関数

f:id:suzuzusu:20190927194603p:plain — 多峰な関数

GPclust

GPclust という混合ガウス過程のライブラリが良さそうなので今回はこれを使用する．

以下コード

gist.github.com

結果

f:id:suzuzusu:20190927194641p:plain

結果の図から多峰な関数を回帰できていることが分かる．

参考

2018-04-18

STDP学習ベースのSNNでMNISTを分類する

機械学習系技術系

雑に論文みて勉強したので何も保証しません．SNNの情報全然無いような気がするのでしんどい．

Spiking Neural Network(SNN)

ニューロンの活動電位(スパイク)に注目したニューラルネットワーク．現状，計算量が多いのでチップを作ったりなどのハードウェアの研究が盛んな傾向にあるような気がする．IBMのTruneNorthとかIntelのLoihiなどはSNNにあたる．

Spike-Timing-Dependent Plasticity(STDP)

STDPはスパイクタイミングに依存してシナプスの重みが変わる仕組みである．ざっくり言うと細胞Aが発火して，細胞Bが発火するとA->B間のシナプス結合が強まるLTP(長期増強)が起きて，逆に細胞Bが発火して，細胞Aが発火するとA->B間のシナプス結合が弱まるLTD(長期抑圧)が起きる．

シナプス前細胞の発火時間を ${t_{pre}}$ ，シナプス後細胞の発火時間を ${t_{post}}$ とする． ${\Delta t}$ を以下のように定義する．

${\displaystyle \Delta t = t_{pre} - t_{post} }$

シナプスの結合の重みの更新は以下の式で表される．STDPの式は色々提案されているが今回は基本的なものを使用する

$stdp$

ニューロンモデル

使用するニューロンモデルは積分発火モデルを使用する．

ネットワーク

入力はMNISTのそれぞれのピクセルデータを最大60Hzのポアソンスパイクモデルにして入力させる．よってneural codingはrate codingを使用する．入力を受け取る興奮性の細胞が発火した場合，他の細胞を抑制させる(winner-take-all)．

f:id:suzuzusu:20180416043913p:plain

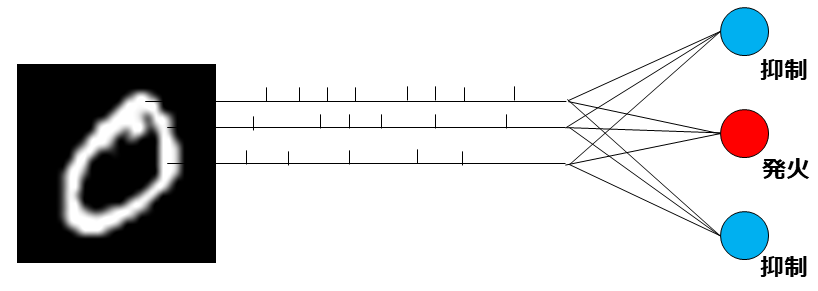
学習後，最終的により多くの反応(発火回数)を示すニューロンをその教師ラベルと紐づける．テストでは，入力に対して最も多くの反応を示したニューロンを抽出し，そのニューロンと紐付けられているラベルと比較する．

結果

以下が学習させた900個のニューロンの重みを表した図である．

f:id:suzuzusu:20180418040907p:plain — weights

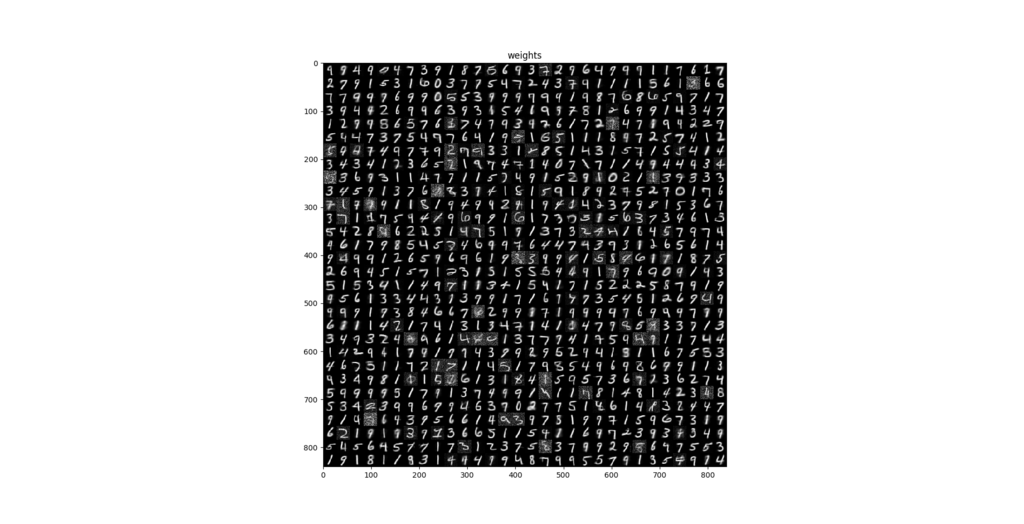
accuracy: 0.775

ソースコード

github.com

参考

2018-04-09

Implementation of Poisson Spike model using Rust

機械学習系技術系

自分用のメモ

実装したニューロンモデル

Poisson Spike model（ポアソンスパイクモデル）

ある時間内に発火する頻度が，ポアソン分布に従うスパイクモデルである．実際のニューロンは不応期などがあり，連続で発火することはないが，このモデルはその辺を考慮していない．ただ，大脳新皮質のスパイクはポアソンスパイクモデルと似たようなスパイクが観測されるらしい．

ポアソン分布は以下のような式で表される．

${\displaystyle P(X=k) = \frac{\lambda^{k}e^{-\lambda}}{k!} }$

$\lambda$ は平均回数を表す．

以下は，ポアソンスパイクモデルの実装

fn generate_spike(fr: f64, dt: f64, t: f64, rng: &mut XorShiftRng) -> Vec<usize> {
    // fr: 発火頻度 Hz
    // dt: 微小量
    // t: 生成する時系列の長さ sec
    let num = (t/dt) as usize;
    let v: Vec<usize> = rng.gen_iter().take(num).map(|x: f64| if x < fr*dt { 1 } else { 0 } ).collect(); // 1が発火を表す
    v
}

例えば $60\mathrm{Hz}$ の発火頻度のポアソンスパイクは1秒間に平均で60回発火が起きる．

以下で $\lambda = 60$ のポアソン分布と1秒間に発火頻度 $60\mathrm{Hz}$ のポアソンスパイクが発火した回数を比較した実験を行った．

extern crate gnuplot;
extern crate rand;

use rand::{Rng, XorShiftRng, SeedableRng};
use rand::distributions::{Poisson, Distribution};

use std::mem::transmute;


pub fn generate_spike(fr: f64, dt: f64, t: f64, rng: &mut XorShiftRng) -> Vec<usize> {
    let num = (t/dt) as usize;
    let v: Vec<usize> = rng.gen_iter().take(num).map(|x: f64| if x < fr*dt { 1 } else { 0 } ).collect();
    v
}

fn main() {
    let seed = 1;
    let x: u32 = 123456789;
    let y: u32 = 362436069;
    let z: u32 = 521288629;
    let w: u32 = seed;
    let seeds: [u32; 4] = [x, y, z, w];
    const N: usize = 1000000;
    const LAMBDA: f64 = 60.0;

    let seeds = unsafe {transmute(seeds)};
    let mut rng = XorShiftRng::from_seed(seeds);
    let mut fg = gnuplot::Figure::new();

    {
        // poisson spike
        let mut spike_cnts = Vec::with_capacity(N);
        for _ in 0..N {
            let spikes = generate_spike(LAMBDA, 0.0001, 1.0, &mut rng);
            let spike_cnt = spikes.iter().sum::<usize>();
            spike_cnts.push(spike_cnt);
        }

        let max_cnt = spike_cnts.iter().max().unwrap();
        let xs = (0..*max_cnt).collect::<Vec<usize>>();

        let mut spike_hist = vec![0;*max_cnt+1];
        for spike_cnt in &spike_cnts {
            spike_hist[*spike_cnt] += 1;
        }

        let ax = fg.axes2d();
        ax.lines(xs.iter(), spike_hist.iter(), &[gnuplot::Caption("poisson spike"), gnuplot::Color("blue")]);


        // poisson distributions
        let mut spike_cnts = Vec::with_capacity(N);
        for _ in 0..N {
            let poi = Poisson::new(LAMBDA);
            let v = poi.sample(&mut rng);
            spike_cnts.push(v);
        }
        let max_cnt = spike_cnts.iter().max().unwrap();

        let mut spike_hist = vec![0;(*max_cnt+1) as usize];
        for spike_cnt in &spike_cnts {
            spike_hist[*spike_cnt as usize] += 1;
        }

        ax.lines(xs.iter(), spike_hist.iter(), &[gnuplot::Caption("poisson distributions"), gnuplot::Color("red")]);

    }
    fg.echo_to_file("ps.plt");
}

f:id:suzuzusu:20180409042017p:plain — 実行結果

良さそう．

github.com

参考

2018-03-27

Implementation of FitzHugh-Nagumo model using Rust

機械学習系技術系

自分用のまとめ

実装したニューロンモデル

FitzHugh-Nagumo（フィッツヒュー・南雲モデル）

HH型モデルを簡略化したモデルである．

${\displaystyle \frac{dV(t)}{dt} = c(-\frac{V(t)^{3}}{3} + V(t) - w + I(t)) \\ \frac{dw}{dt} = V(t) - bw +a \\ }$

それぞれのパラメータは以下を参考にして次のように設定した．

http://www.chem.scphys.kyoto-u.ac.jp/nonnonWWW/b8/07f/majima/majima.pdf

${ \displaystyle a = 0.7 \\ b = 0.8 \\ c = 10 \\ }$

初期値問題にはルンゲ＝クッタ法を使用した．以下実装したコード

extern crate gnuplot;

fn rk4<F: Fn(f64)->f64>(f: F, y: f64, dt: f64) -> f64 {
    let k1 = dt * f(y);
    let k2 = dt * f(y + k1*0.5);
    let k3 = dt * f(y + k2*0.5);
    let k4 = dt * f(y + k3);
    (k1 + 2.0*k2 + 2.0*k3 + k4) / 6.0
}

fn main(){
    const A: f64 = 0.7;
    const B: f64 = 0.8;
    const C: f64 = 10.0;

    let mut t = -30.0;
    let dt = 0.001;
    let mut v = 0.0;
    let mut w = 0.0;
    let mut i_ext ;

    let mut x = Vec::new();
    let mut y = Vec::new();

    while t <= 100.0 {

        if t >= 30.0 && t <= 70.0 {
            i_ext = 0.35;
        } else {
            i_ext = 0.0;
        }

        let d_w = move |y:f64| v - B * y + A;
        w += rk4(d_w, w, dt);

        let d_v = move |y:f64| C*(-y.powf(3.0)/3.0 + y - w + i_ext);
        v += rk4(d_v, v, dt);

        if t >= 0.0 {
            y.push(v);
            x.push(t);
        }

        t += dt;
    }

    let mut fg = gnuplot::Figure::new();
    fg.axes2d().lines(x.iter(), y.iter(), &[gnuplot::Color("blue")]);
    fg.echo_to_file("fn.plt");
}

f:id:suzuzusu:20180327092810p:plain — 実行結果

github.com

参考

http://www.chem.scphys.kyoto-u.ac.jp/nonnonWWW/b8/07f/majima/majima.pdf

2018-03-25

Implementation of Integrate-and-fire model using Rust

機械学習系技術系

自分用のまとめ

実装したニューロンモデル

Integrate-and-fire（積分発火モデル）

入力の時間積分によって細胞の膜電位が増加し，ある閾値を超えるとスパイクが生成されるという現象を再現したモデルである． HH型モデルのような生物的なニューロンモデルとは異なった挙動をするので注意する必要がある．

${\displaystyle \tau \frac{dV(t)}{dt} = E_{L} - V(t) + RI(t) \\ if\ V(t) \geq V_{\theta} \ then \ V(t) = V_{0} }$

それぞれの定数は以下のように設定した．

${ \displaystyle E_{L} = -65 \\ \tau = 10 \\ V_{\theta} = -55 \\ RI = 12 }$

初期値問題にはルンゲ＝クッタ法を使用した．以下実装したコード

extern crate gnuplot;

fn rk4<F: Fn(f64)->f64>(f: F, y: f64, dt: f64) -> f64 {
    let k1 = dt * f(y);
    let k2 = dt * f(y + k1*0.5);
    let k3 = dt * f(y + k2*0.5);
    let k4 = dt * f(y + k3);
    (k1 + 2.0*k2 + 2.0*k3 + k4) / 6.0
}

fn main(){
    const E_L: f64 = -65.0;
    const THETA: f64 = -55.0;
    const TAU: f64 = 10.0;
    const RI: f64 = 12.0;

    let mut t = 0.0;
    let dt = 0.001;
    let mut v = E_L;

    let mut x = Vec::new();
    let mut y = Vec::new();

    while t <= 100.0 {

        if v >= THETA {
            v = E_L;
        }

        let d_v = move |y:f64| (E_L - y + RI)/TAU;
        v += rk4(d_v, v, dt);

        y.push(v);
        x.push(t);

        t += dt;
    }

    let mut fg = gnuplot::Figure::new();
    fg.axes2d().lines(x.iter(), y.iter(), &[gnuplot::Color("blue")]);
    fg.echo_to_file("if.plt");
}

github.com

2018-03-25

Implementation of Izhikevich model using Rust

機械学習系技術系

自分用のまとめ

実装したニューロンモデル

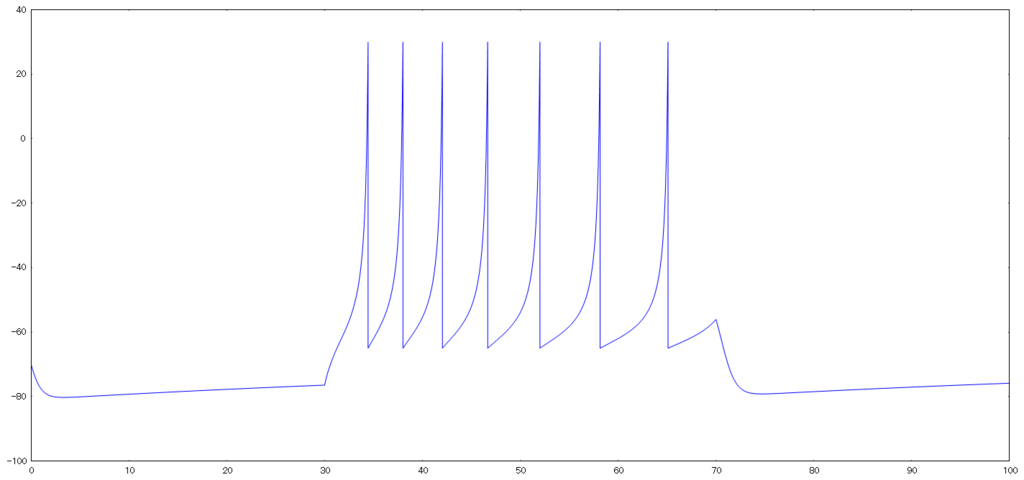
Izhikevich（イジケヴィッチモデル）

Hodgkin–Huxley modelなどのコンダクタンス依存型モデルは複雑な式で計算量もそれなりにいるので，簡易な形に落とし込んだモデルがIzhikevich modelである．以下のような2変数の常微分方程式で表すことができる．

${ \displaystyle \frac{dv}{dt} = 0.04v^{2} + 5v + 140 - bu + I \\ \frac{du}{dt} = a(v-u) }$

ここで変数 ${v(t)}$ と ${u(t)}$ は，Izニューロンが発火するたびに以下のような規則で状態を更新する．

${v(t)}$ の値が30になった場合， ${v(t)}$ の値をcにし， ${u(t)}$ に ${d}$ を加算する．

if v = 30 mV
then v <- c, u <- u+d

それぞれの定数は以下のように設定した．

${ \displaystyle a = 0.02 \\ b = 0.2 \\ c = -65 \\ d = 40 }$

初期値問題にはルンゲ＝クッタ法を使用した．以下実装したコード

extern crate gnuplot;

fn rk4<F: Fn(f64)->f64>(f: F, y: f64, dt: f64) -> f64 {
    let k1 = dt * f(y);
    let k2 = dt * f(y + k1*0.5);
    let k3 = dt * f(y + k2*0.5);
    let k4 = dt * f(y + k3);
    (k1 + 2.0*k2 + 2.0*k3 + k4) / 6.0
}

fn main(){
    const A: f64 = 0.02;
    const B: f64 = 0.2;
    const C: f64 = -65.0;
    const D: f64 = 6.0;

    let mut t = -0.0;
    let dt = 0.001;
    let mut i_ext ;
    let mut v = -70.0;
    let mut u = B*v;

    let mut x = Vec::new();
    let mut y = Vec::new();

    while t <= 100.0 {

        if t > 30.0 && t < 70.0 {
            i_ext = 14.0;
        } else {
            i_ext = 0.0;
        }

        let d_v = move |y:f64| 0.04*y*y+5.0*y+140.0-B*u+i_ext;
        v += rk4(d_v, v, dt);

        let d_u = move |y:f64| A*(v - y);
        u += rk4(d_u, u, dt);

        if v > 30.0 {
            y.push(30.0);
            v = C;
            u += D;
        }else {
            y.push(v);
        }
        x.push(t);

        t += dt;
    }

    let mut fg = gnuplot::Figure::new();
    fg.axes2d().lines(x.iter(), y.iter(), &[gnuplot::Color("blue")]);
    fg.echo_to_file("iz.plt");
}

f:id:suzuzusu:20180325123127p:plain — 実行結果

github.com

参考

Which Model to Use for Cortical Spiking Neurons?
Fundamentals of Computational Neuroscience
脳の計算論

2018-03-25

Implementation of Hodgkin–Huxley model using Rust

機械学習系技術系

自分用のまとめ

実装したニューロンモデル

Hodgkin–Huxley model（ホジキン・ハクスレーモデル）

神経細胞の細胞膜をコンデンサ，イオンチャネルを変化する抵抗素子として考えた電気回路モデル（回路図は割愛）である．ナトリウム，カリウムを通すイオンチャネルが存在し，それぞれに平衡電位を持つ．

キルヒホッフの法則の法則から以下の式が成り立つ．

${ \displaystyle C \frac{dV(t)}{dt} = -I_{Na}(t) - I_{K}(t) - I_{L}(t) + I(t) }$

${I_{Na}}$ ， ${I_{K}}$ はナトリウムチャンネル，カリウムチャンネルが通り流れ出す電流で， ${I_{L}}$ は漏れ電流である．

それぞれの電流は以下の式で表される．

${ \displaystyle I_{Na}(t) = g_{Na}m(t)^{3} h(t)(V(t) - E_{Na}) \\ I_{K}(t) = g_{K}n(t)^{4}(V(t) - E_{K}) \\ I_{L}(t) = g_{L}(V(t) - E_{L}) }$

変数 ${h, m, n}$ は以下のxを読み替えた同じ式に従う．

${ \displaystyle \alpha_{x}(V)(1-x(t)) - \beta_{x}(V)x(t) }$

${ \displaystyle \alpha_{h}(V) = 0.07 \exp(\frac{-V}{20}) \\ \alpha_{m}(V) = \frac{0.1(25-V)}{\exp\left\{(25-V)/10\right\}-1} \\ \alpha_{n}(V) = \frac{0.01(10-V)}{\exp\left\{(10-V)/10\right\}-1} \\ \beta_{h}(V) = \frac{1}{\exp\left\{(30-V)/10\right\}+1} \\ \beta_{m}(V) = 4 \exp(\frac{-V}{18}) \\ \beta_{n}(V) = 0.125 \exp(\frac{-V}{80}) \\ }$

それぞれの定数は以下のように設定した．

${ \displaystyle E_{Na} = 115 mV \\ E_{K} = -12 mV \\ E_{L} = 10.613 mV \\ g_{Na} = 120 mV \\ g_{K} = 36 mV \\ g_{L} = 0.3 mV \\ C_{m} = 1.0 \mu F / cm^{2} \\ }$

初期値問題にはルンゲ＝クッタ法を使用した．以下実装したコード

extern crate gnuplot;

fn alpha_m(v: f64) -> f64{
    (0.1*(25.0-v)) / (((25.0-v)/10.0).exp()-1.0)
}

fn alpha_h(v: f64) -> f64{
    0.07*((-v/20.0).exp())
}

fn alpha_n(v: f64) -> f64{
    (0.01*(10.0-v)) / (((10.0-v)/10.0).exp()-1.0)
}

fn beta_m(v: f64) -> f64{
    4.0*((-v/18.0).exp())
}

fn beta_h(v: f64) -> f64{
    1.0/(((30.0-v)/10.0).exp()+1.0)
}

fn beta_n(v: f64) -> f64{
    0.125*((-v/80.0).exp())
}

fn rk4<F: Fn(f64)->f64>(f: F, y: f64, dt: f64) -> f64 {
    let k1 = dt * f(y);
    let k2 = dt * f(y + k1*0.5);
    let k3 = dt * f(y + k2*0.5);
    let k4 = dt * f(y + k3);
    (k1 + 2.0*k2 + 2.0*k3 + k4) / 6.0
}

fn main(){
    const E_NA: f64 = 115.0;
    const E_K:  f64 = -12.0;
    const E_L:  f64 = 10.613;
    const G_NA: f64 = 120.0;
    const G_K:  f64 = 36.0;
    const G_L:  f64 = 0.3;
    const C_M:  f64 = 1.0;

    let mut t = -100.0;
    let dt = 0.001;
    let mut i_ext ;
    let mut v = -10.0;
    let mut x_n = 0.0;
    let mut x_m = 0.0;
    let mut x_h = 0.0;

    let mut x = Vec::new();
    let mut y = Vec::new();

    while t <= 100.0 {

        if t > 30.0 && t < 70.0 {
            i_ext = 10.0;
        } else {
            i_ext = 0.0;
        }

        let a_n = alpha_n(v);
        let a_m = alpha_m(v);
        let a_h = alpha_h(v);

        let b_n = beta_n(v);
        let b_m = beta_m(v);
        let b_h = beta_h(v);

        let d_n = |y: f64| a_n*(1.0-y) - b_n*y;
        let d_m = |y: f64| a_m*(1.0-y) - b_m*y;
        let d_h = |y: f64| a_h*(1.0-y) - b_h*y;

        x_n += rk4(d_n, x_n, dt);
        x_m += rk4(d_m, x_m, dt);
        x_h += rk4(d_h, x_h, dt);

        let i_na = G_NA *(x_m.powf(3.0))*x_h*(v- E_NA);
        let i_k = G_K *(x_n.powf(4.0))*(v- E_K);
        let i_l = G_L *(v- E_L);
        let i_sum = i_na + i_k + i_l;

        let d_v = |y:f64| (i_ext - i_sum) / C_M;
        v += rk4(d_v, v, dt);

        if t >= 0.0{
            x.push(t);
            y.push(v);
        }
        t += dt;
    }

    let mut fg = gnuplot::Figure::new();
    fg.axes2d().lines(x.iter(), y.iter(), &[gnuplot::Color("blue")]);
    fg.echo_to_file("hh.plt");
}

f:id:suzuzusu:20180325110018p:plain — 実行結果

github.com

参考

Fundamentals of Computational Neuroscience
脳の計算論

suzuzusu日記

(´･ω･｀)

混合ガウス過程で多峰な関数を回帰する

混合ガウス過程と多峰な関数

GPclust

結果

参考

STDP学習ベースのSNNでMNISTを分類する

Spiking Neural Network(SNN)

Spike-Timing-Dependent Plasticity(STDP)

ニューロンモデル

ネットワーク

結果

ソースコード

参考

Implementation of Poisson Spike model using Rust

Poisson Spike model（ポアソンスパイクモデル）

参考

Implementation of FitzHugh-Nagumo model using Rust

FitzHugh-Nagumo（フィッツヒュー・南雲モデル）

参考

Implementation of Integrate-and-fire model using Rust

Integrate-and-fire（積分発火モデル）

Implementation of Izhikevich model using Rust

Izhikevich（イジケヴィッチモデル）

参考

Implementation of Hodgkin–Huxley model using Rust

Hodgkin–Huxley model（ホジキン・ハクスレーモデル）

参考