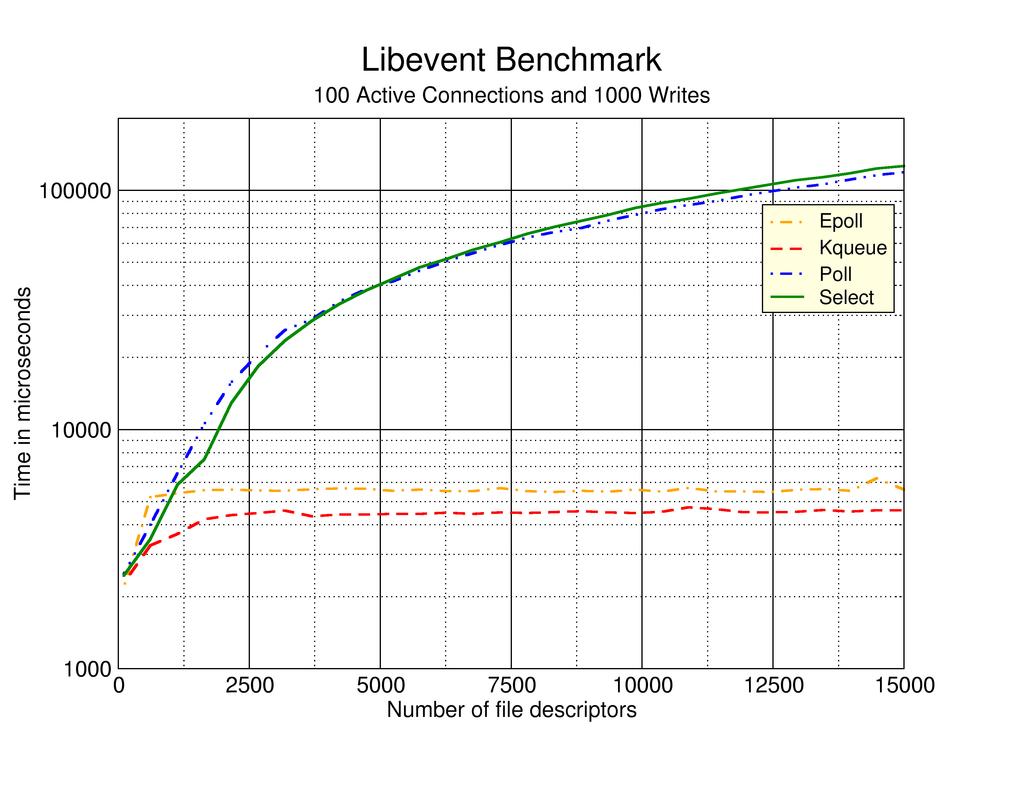
fork, select, poll, epoll, io_uringのecho server
fork, select, poll, epoll, io_uringなどを使用してそれぞれecho serverを実装したのでそれぞれの仕様などを忘備録としてまとめていきます。エラー処理とか雑な部分があると思いますがご容赦ください。
環境構築
macOS上での実行を前提にします。io_uringを使う場合にはlinux kernel 5.1以上でないと動かないので、multipassというubuntuのVMを手軽に作成できるツールを使って実行環境を構築します。
multipassのインストール
brew install --cask multipass
20.10のubuntuを用意して、gccやio_uringのライブラリであるliburingを入れます。
multipass launch 20.10 -n primary multipass shell # login sudo apt update -y sudo apt install gcc liburing -y uname -a > Linux primary 5.8.0-43-generic #49-Ubuntu SMP Fri Feb 5 03:01:28 UTC 2021 x86_64 x86_64 x86_64 GNU/Linux
fork
forkを使用したサーバでは、1クライアントに1プロセスが対応することになり、メモリが枯渇して性能に余裕があるのにもかかわらずレスポンス性能が大きく落ちます。
有名なC10K問題を引き起こします。
C10K問題(英語: C10K problem)とは、Apache HTTP ServerなどのWebサーバソフトウェアとクライアントの通信において、クライアントが約1万台に達すると、Webサーバーのハードウェア性能に余裕があるにも関わらず、レスポンス性能が大きく下がる問題である。
#include <arpa/inet.h> #include <signal.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/socket.h> #include <unistd.h> #define BACKLOG_SIZE 5 #define BUF_SIZE 1024 #define INF_TIME -1 #define DISABLE -1 int listen_fd; void int_handle(int n) { close(listen_fd); exit(EXIT_SUCCESS); } // wirte n byte ssize_t write_n(int fd, char *ptr, size_t n) { ssize_t n_left = n, n_written; while (n_left > 0) { if ((n_written = write(fd, ptr, n_left)) <= 0) { return n_written; } n_left -= n_written; ptr += n_written; } return EXIT_SUCCESS; } int main(int argc, char **argv) { // Create listen socket if ((listen_fd = socket(AF_INET, SOCK_STREAM, 0)) < 0) { fprintf(stderr, "Error: socket\n"); return EXIT_FAILURE; } // TCP port number int port = 8080; // Initialize server socket address struct sockaddr_in server_addr; memset(&server_addr, 0, sizeof(server_addr)); server_addr.sin_family = AF_INET; server_addr.sin_addr.s_addr = INADDR_ANY; server_addr.sin_port = htons(port); // Bind socket to an address if (bind(listen_fd, (struct sockaddr *)&server_addr, sizeof(server_addr)) < 0) { fprintf(stderr, "Error: bind\n"); return EXIT_FAILURE; } // Listen if (listen(listen_fd, BACKLOG_SIZE) < 0) { fprintf(stderr, "Error: listen\n"); return EXIT_FAILURE; } // Set INT signal handler signal(SIGINT, int_handle); fprintf(stderr, "listen on port %d\n", port); while (1) { // Check new connection struct sockaddr_in client_addr; socklen_t len_client = sizeof(client_addr); int conn_fd; if ((conn_fd = accept(listen_fd, (struct sockaddr *)&client_addr, &len_client)) < 0) { fprintf(stderr, "Error: accept\n"); return EXIT_FAILURE; } printf("Accept socket %d (%s : %hu)\n", conn_fd, inet_ntoa(client_addr.sin_addr), ntohs(client_addr.sin_port)); pid_t pid = fork(); if (pid < 0) { fprintf(stderr, "Error: fork\n"); return EXIT_FAILURE; } if (pid == 0) { // child char buf[BUF_SIZE]; close(listen_fd); while (1) { ssize_t n = read(conn_fd, buf, BUF_SIZE); if (n < 0) { fprintf(stderr, "Error: read from socket %d\n", conn_fd); close(conn_fd); exit(-1); } else if (n == 0) { // connection closed by client printf("Close socket %d\n", conn_fd); close(conn_fd); exit(0); } else { printf("Read %zu bytes from socket %d\n", n, conn_fd); write_n(conn_fd, buf, n); } } } else { // parent close(conn_fd); } } close(listen_fd); return EXIT_SUCCESS; }
I/O多重化
上記のようなマルチプロセスにより起きるC10K問題を解決する方法として、クライアント数にかかわらず1プロセスで処理するイベント駆動型プログラミングが提案されています。
イベント駆動型プログラミング(イベントくどうがたプログラミング、英: event-driven programming)は、コンピュータプログラムが起動すると共にイベントを待機し、発生したイベントに従って受動的に処理を行うプログラミングパラダイムのこと。
以降はI/O多重化によるecho serverを実装していきます。I/O多重化とは複数のI/Oデバイスの状態を同時に監視する仕組みです。例えば1プロセスで複数のクライアントを制御するためにこの技術は使用されます。
select
ディスクリプタを線形に探索する必要があるので計算量がO(n)かかります。管理できるディスクリプタ数に上限があるのが特徴です。
#include <arpa/inet.h> #include <errno.h> #include <signal.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/select.h> #include <sys/socket.h> #include <unistd.h> #define BACKLOG_SIZE 5 #define BUF_SIZE 1024 #define N_CLIENT 256 #define INF_TIME -1 #define DISABLE -1 int listen_fd; void int_handle(int n) { close(listen_fd); exit(EXIT_SUCCESS); } // wirte n byte ssize_t write_n(int fd, char *ptr, size_t n) { ssize_t n_left = n, n_written; while (n_left > 0) { if ((n_written = write(fd, ptr, n_left)) <= 0) { return n_written; } n_left -= n_written; ptr += n_written; } return EXIT_SUCCESS; } int main(int argc, char **argv) { char buf[BUF_SIZE]; fd_set fds; FD_ZERO(&fds); int clients[N_CLIENT]; for (int i = 0; i < N_CLIENT; i++) { clients[i] = DISABLE; } memset(&fds, 0, sizeof(fds)); // Create listen socket if ((listen_fd = socket(AF_INET, SOCK_STREAM, 0)) < 0) { fprintf(stderr, "Error: socket\n"); return EXIT_FAILURE; } // Set INT signal handler signal(SIGINT, int_handle); // TCP port number int port = 8080; // Initialize server socket address struct sockaddr_in server_addr; memset(&server_addr, 0, sizeof(server_addr)); server_addr.sin_family = AF_INET; server_addr.sin_addr.s_addr = INADDR_ANY; server_addr.sin_port = htons(port); // Bind socket to an address if (bind(listen_fd, (struct sockaddr *)&server_addr, sizeof(server_addr)) < 0) { fprintf(stderr, "Error: bind\n"); return EXIT_FAILURE; } // Listen if (listen(listen_fd, BACKLOG_SIZE) < 0) { fprintf(stderr, "Error: listen\n"); return EXIT_FAILURE; } fprintf(stderr, "listen on port %d\n", port); FD_SET(listen_fd, &fds); int max_fd = listen_fd; // max fd int max_i = 0; // max client into clients[] array while (1) { FD_ZERO(&fds); FD_SET(listen_fd, &fds); for (int i = 0; i < N_CLIENT; i++) { if (clients[i] != DISABLE) { FD_SET(clients[i], &fds); } } int res_select = select(max_fd + 1, &fds, NULL, NULL, NULL); if (res_select < 0) { fprintf(stderr, "Error: select"); return EXIT_FAILURE; } // Check new connection if (FD_ISSET(listen_fd, &fds)) { struct sockaddr_in client_addr; socklen_t len_client = sizeof(client_addr); int connfd; if ((connfd = accept(listen_fd, (struct sockaddr *)&client_addr, &len_client)) < 0) { fprintf(stderr, "Error: accept\n"); return EXIT_FAILURE; } printf("Accept socket %d (%s : %hu)\n", connfd, inet_ntoa(client_addr.sin_addr), ntohs(client_addr.sin_port)); // Save client socket into clients array int i; for (i = 0; i < N_CLIENT; i++) { if (clients[i] == DISABLE) { clients[i] = connfd; break; } } // No enough space in clients array if (i == N_CLIENT) { fprintf(stderr, "Error: too many clients\n"); close(connfd); } if (i > max_i) { max_i = i; } if (connfd > max_fd) { max_fd = connfd; } } // Check all clients to read data for (int i = 0; i <= max_i; i++) { int sock_fd; if ((sock_fd = clients[i]) == DISABLE) { continue; } // If the client is readable or errors occur ssize_t n = read(sock_fd, buf, BUF_SIZE); if (n < 0) { fprintf(stderr, "Error: read from socket %d\n", sock_fd); close(sock_fd); clients[i] = DISABLE; } else if (n == 0) { // connection closed by client printf("Close socket %d\n", sock_fd); close(sock_fd); clients[i] = DISABLE; } else { printf("Read %zu bytes from socket %d\n", n, sock_fd); write_n(sock_fd, buf, n); write_n(1, buf, n); } } } close(listen_fd); return EXIT_SUCCESS; }
poll
selectとほとんど同じ機能であり、計算量も同じO(n)だけかかります。ただし、管理するディスクリプタの制限がない点で上位互換と捉えることができます。
#include <arpa/inet.h> #include <errno.h> #include <poll.h> #include <signal.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/socket.h> #include <unistd.h> #define BACKLOG_SIZE 5 #define BUF_SIZE 1024 #define N_CLIENT 256 #define INF_TIME -1 #define DISABLE -1 int listen_fd; void int_handle(int n) { close(listen_fd); exit(EXIT_SUCCESS); } // wirte n byte ssize_t write_n(int fd, char *ptr, size_t n) { ssize_t n_left = n, n_written; while (n_left > 0) { if ((n_written = write(fd, ptr, n_left)) <= 0) { return n_written; } n_left -= n_written; ptr += n_written; } return EXIT_SUCCESS; } int main(int argc, char **argv) { char buf[BUF_SIZE]; struct pollfd clients[N_CLIENT]; // Create listen socket if ((listen_fd = socket(AF_INET, SOCK_STREAM, 0)) < 0) { fprintf(stderr, "Error: socket\n"); return EXIT_FAILURE; } // TCP port number int port = 8080; // Initialize server socket address struct sockaddr_in server_addr; memset(&server_addr, 0, sizeof(server_addr)); server_addr.sin_family = AF_INET; server_addr.sin_addr.s_addr = INADDR_ANY; server_addr.sin_port = htons(port); // Bind socket to an address if (bind(listen_fd, (struct sockaddr *)&server_addr, sizeof(server_addr)) < 0) { fprintf(stderr, "Error: bind\n"); return EXIT_FAILURE; } // Listen if (listen(listen_fd, BACKLOG_SIZE) < 0) { fprintf(stderr, "Error: listen\n"); return EXIT_FAILURE; } // Set INT signal handler signal(SIGINT, int_handle); fprintf(stderr, "listen on port %d\n", port); clients[0].fd = listen_fd; clients[0].events = POLLIN; for (int i = 1; i < N_CLIENT; i++) { clients[i].fd = DISABLE; } int max_i = 0; // max index into clients[] array while (1) { int n_ready = poll(clients, max_i + 1, INF_TIME); // Time out if (n_ready == 0) { continue; } // Error poll if (n_ready < 0) { fprintf(stderr, "Error: poll %d\n", errno); return errno; } // Check new connection if (clients[0].revents & POLLIN) { struct sockaddr_in client_addr; socklen_t len_client = sizeof(client_addr); int connfd; if ((connfd = accept(listen_fd, (struct sockaddr *)&client_addr, &len_client)) < 0) { fprintf(stderr, "Error: accept\n"); return EXIT_FAILURE; } printf("Accept socket %d (%s : %hu)\n", connfd, inet_ntoa(client_addr.sin_addr), ntohs(client_addr.sin_port)); // Save client socket into clients array int i; for (i = 0; i < N_CLIENT; i++) { if (clients[i].fd == DISABLE) { clients[i].fd = connfd; break; } } // No enough space in clients array if (i == N_CLIENT) { fprintf(stderr, "Error: too many clients\n"); close(connfd); } clients[i].events = POLLIN; if (i > max_i) { max_i = i; } } // Check all clients to read data for (int i = 1; i <= max_i; i++) { int sock_fd; if ((sock_fd = clients[i].fd) == DISABLE) { continue; } // If the client is readable or errors occur if (clients[i].revents & (POLLIN | POLLERR)) { ssize_t n = read(sock_fd, buf, BUF_SIZE); if (n < 0) { fprintf(stderr, "Error: read from socket %d\n", sock_fd); close(sock_fd); clients[i].fd = DISABLE; } else if (n == 0) { // connection closed by client printf("Close socket %d\n", sock_fd); close(sock_fd); clients[i].fd = DISABLE; } else { printf("Read %zu bytes from socket %d\n", n, sock_fd); write_n(sock_fd, buf, n); write_n(1, buf, n); } } } } close(listen_fd); return EXIT_SUCCESS; }
epoll
linux kernel 2.6以降であれば使用可能なAPIです。
ディスクリプタの状態をカーネル空間で監視しているため、直接変更のあるディスクリプタを返してくれるので計算量がO(1)となり高速に処理できます。
ただし、ディスクリプタが1の場合はepollにオーバーヘッドが存在して、pollの方が早い場合もあるので注意が必要です。
#include <arpa/inet.h> #include <errno.h> #include <signal.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/epoll.h> #include <sys/socket.h> #include <unistd.h> #define BACKLOG_SIZE 5 #define BUF_SIZE 1024 #define N_CLIENT 256 #define INF_TIME -1 #define DISABLE -1 int listen_fd; void int_handle(int n) { close(listen_fd); exit(EXIT_SUCCESS); } // wirte n byte ssize_t write_n(int fd, char *ptr, size_t n) { ssize_t n_left = n, n_written; while (n_left > 0) { if ((n_written = write(fd, ptr, n_left)) <= 0) { return n_written; } n_left -= n_written; ptr += n_written; } return EXIT_SUCCESS; } int main(int argc, char **argv) { char buf[BUF_SIZE]; // Create listen socket if ((listen_fd = socket(AF_INET, SOCK_STREAM, 0)) < 0) { fprintf(stderr, "Error: socket\n"); return EXIT_FAILURE; } // TCP port number int port = 8080; // Initialize server socket address struct sockaddr_in server_addr; memset(&server_addr, 0, sizeof(server_addr)); server_addr.sin_family = AF_INET; server_addr.sin_addr.s_addr = INADDR_ANY; server_addr.sin_port = htons(port); // Bind socket to an address if (bind(listen_fd, (struct sockaddr *)&server_addr, sizeof(server_addr)) < 0) { fprintf(stderr, "Error: bind\n"); return EXIT_FAILURE; } // Listen if (listen(listen_fd, BACKLOG_SIZE) < 0) { fprintf(stderr, "Error: listen\n"); return EXIT_FAILURE; } // Set INT signal handler signal(SIGINT, int_handle); fprintf(stderr, "listen on port %d\n", port); // Create epoll int epfd = epoll_create1(0); if (epfd < 0) { fprintf(stderr, "Error: epoll create\n"); close(listen_fd); return EXIT_FAILURE; } struct epoll_event listen_ev; memset(&listen_ev, 0, sizeof(listen_ev)); listen_ev.events = EPOLLIN; listen_ev.data.fd = listen_fd; if (epoll_ctl(epfd, EPOLL_CTL_ADD, listen_fd, &listen_ev) < 0) { fprintf(stderr, "Error: epoll ctl add listen\n"); close(listen_fd); return EXIT_FAILURE; } struct epoll_event evs[N_CLIENT]; while (1) { // Wait epoll listener int n_fds = epoll_wait(epfd, evs, N_CLIENT, -1); // Error epoll if (n_fds < 0) { fprintf(stderr, "Error: epoll wait\n"); close(listen_fd); return EXIT_FAILURE; } for (int i = 0; i < n_fds; i++) { if (evs[i].data.fd == listen_fd) { // Add epoll listener struct sockaddr_in client_addr; socklen_t len_client = sizeof(client_addr); int conn_fd; if ((conn_fd = accept(listen_fd, (struct sockaddr *)&client_addr, &len_client)) < 0) { fprintf(stderr, "Error: accept\n"); return EXIT_FAILURE; } printf("Accept socket %d (%s : %hu)\n", conn_fd, inet_ntoa(client_addr.sin_addr), ntohs(client_addr.sin_port)); struct epoll_event conn_ev; memset(&conn_ev, 0, sizeof(listen_ev)); conn_ev.events = EPOLLIN; conn_ev.data.fd = conn_fd; if (epoll_ctl(epfd, EPOLL_CTL_ADD, conn_fd, &conn_ev) < 0) { fprintf(stderr, "Error: epoll ctl add listen\n"); close(listen_fd); return EXIT_FAILURE; } } else if (evs[i].events & EPOLLIN) { // Read data from client int sock_fd = evs[i].data.fd; ssize_t n = read(sock_fd, buf, BUF_SIZE); if (n < 0) { fprintf(stderr, "Error: read from socket %d\n", sock_fd); close(sock_fd); } else if (n == 0) { // connection closed by client printf("Close socket %d\n", sock_fd); struct epoll_event sock_ev; memset(&sock_ev, 0, sizeof(listen_ev)); sock_ev.events = EPOLLIN; sock_ev.data.fd = sock_fd; if (epoll_ctl(epfd, EPOLL_CTL_DEL, sock_fd, &sock_ev) < 0) { fprintf(stderr, "Error: epoll ctl dell\n"); close(listen_fd); return EXIT_FAILURE; } close(sock_fd); } else { printf("Read %zu bytes from socket %d\n", n, sock_fd); write_n(sock_fd, buf, n); write_n(1, buf, n); } } } } close(listen_fd); return EXIT_SUCCESS; }
io_uring
https://kernel.dk/io_uring.pdf
linux kernel 5.1以降であれば使用可能な新しい非同期I/O APIです。submission queue (SQ)とcompletion queue (CQ)の二つのring bufferを操作することで処理をします。例えばソケットからメッセージを受け取るrecvmsg を実行するためには IORING_OP_RECVMSG opcodeのsubmission queue entry (SQE)をSQに投入することで処理が非同期で実行されます。またそれらの処理の完了通知はCQからcompletion queue entry (CQE)を受け取ることで実現できます。
今回はliburing というio_uringのシンプルなインターフェイスを提供しているライブラリを使用して実装します。
#include <arpa/inet.h> #include <errno.h> #include <liburing.h> #include <signal.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/socket.h> #include <unistd.h> #define BACKLOG_SIZE 5 #define BUF_SIZE 1024 #define N_CLIENT 256 #define N_ENTRY 2048 #define GID 1 int listen_fd; enum { ACCEPT, READ, WRITE, }; typedef struct UserData { __u32 fd; __u16 type; } UserData; void int_handle(int n) { close(listen_fd); exit(EXIT_SUCCESS); } // wirte n byte ssize_t write_n(int fd, char *ptr, size_t n) { ssize_t n_left = n, n_written; while (n_left > 0) { if ((n_written = write(fd, ptr, n_left)) <= 0) { return n_written; } n_left -= n_written; ptr += n_written; } return EXIT_SUCCESS; } int main(int argc, char **argv) { char buf[BUF_SIZE] = {0}; // Create listen socket if ((listen_fd = socket(AF_INET, SOCK_STREAM, 0)) < 0) { fprintf(stderr, "Error: socket\n"); return EXIT_FAILURE; } // TCP port number int port = 8080; // Initialize server socket address struct sockaddr_in server_addr, client_addr; socklen_t client_len = sizeof(client_addr); memset(&server_addr, 0, sizeof(server_addr)); server_addr.sin_family = AF_INET; server_addr.sin_addr.s_addr = INADDR_ANY; server_addr.sin_port = htons(port); // Bind socket to an address if (bind(listen_fd, (struct sockaddr *)&server_addr, sizeof(server_addr)) < 0) { fprintf(stderr, "Error: bind\n"); return EXIT_FAILURE; } // Listen if (listen(listen_fd, BACKLOG_SIZE) < 0) { fprintf(stderr, "Error: listen\n"); return EXIT_FAILURE; } // Set INT signal handler signal(SIGINT, int_handle); fprintf(stderr, "listen on port %d\n", port); // Initialize io_uring struct io_uring ring; struct io_uring_sqe *sqe; struct io_uring_cqe *cqe; int init_ret = io_uring_queue_init(N_ENTRY, &ring, 0); if (init_ret < 0) { fprintf(stderr, "Error: init io_uring queue %d\n", init_ret); close(listen_fd); return EXIT_FAILURE; } // Setup first accept sqe = io_uring_get_sqe(&ring); io_uring_prep_accept(sqe, listen_fd, (struct sockaddr *)&client_addr, &client_len, 0); io_uring_sqe_set_flags(sqe, 0); UserData conn_info = { .fd = listen_fd, .type = ACCEPT, }; memcpy(&sqe->user_data, &conn_info, sizeof(conn_info)); while (1) { io_uring_submit(&ring); io_uring_wait_cqe(&ring, &cqe); struct UserData conn_info; memcpy(&conn_info, &cqe->user_data, sizeof(conn_info)); int type = conn_info.type; if (cqe->res == -ENOBUFS) { fprintf(stderr, "Error: no buffer %d\n", cqe->res); close(listen_fd); return EXIT_FAILURE; } else if (type == ACCEPT) { int conn_fd = cqe->res; printf("Accept socket %d \n", conn_fd); if (conn_fd >= 0) { // no error // Read from client sqe = io_uring_get_sqe(&ring); io_uring_prep_recv(sqe, conn_fd, buf, BUF_SIZE, 0); UserData read_info = { .fd = conn_fd, .type = READ, }; memcpy(&sqe->user_data, &read_info, sizeof(read_info)); } // Add new client sqe = io_uring_get_sqe(&ring); io_uring_prep_accept(sqe, listen_fd, (struct sockaddr *)&client_addr, &client_len, 0); io_uring_sqe_set_flags(sqe, 0); UserData conn_info = { .fd = listen_fd, .type = ACCEPT, }; memcpy(&sqe->user_data, &conn_info, sizeof(conn_info)); } else if (type == READ) { int n_byte = cqe->res; if (cqe->res <= 0) { // connection closed by client printf("Close socket %d\n", conn_info.fd); close(conn_info.fd); } else { // Add Write printf("Read %d bytes from socket %d\n", n_byte, conn_info.fd); sqe = io_uring_get_sqe(&ring); io_uring_prep_send(sqe, conn_info.fd, buf, n_byte, 0); write_n(1, buf, n_byte); // output stdout io_uring_sqe_set_flags(sqe, 0); UserData write_info = { .fd = conn_info.fd, .type = WRITE, }; memcpy(&sqe->user_data, &write_info, sizeof(write_info)); } } else if (type == WRITE) { // Add read sqe = io_uring_get_sqe(&ring); io_uring_prep_recv(sqe, conn_info.fd, buf, BUF_SIZE, 0); UserData read_info = { .fd = conn_info.fd, .type = READ, }; memcpy(&sqe->user_data, &read_info, sizeof(read_info)); } io_uring_cqe_seen(&ring, cqe); } close(listen_fd); return EXIT_SUCCESS; }
repository
実装したecho serverは、以下のrepositoryに置きました
参考
Navigable Small Worldによる近似最近傍探索
Small World Networkのグラフ特性を利用したNavigable Small World(NSW)というグラフベースの近似最近傍探索をjuliaで実装します
Navigable Small Worldとは?

上記の画像のようにSmall World Networkの特性を持つグラフベースの検索インデックスからqueryに対して近傍のノードを返すアルゴリズムです。 これを階層的に拡張したHierarchical Navigable Small World(HNSW)は非常に性能が良い近似最近傍探索アルゴリズムとして知られています。
実装
まず、n次元のデータ data と隣接ノード friend を持つ Node 構造体を作ります。
using Random using LinearAlgebra using DataStructures using Base mutable struct Node data friend::Set{Node} end function show(io::IO, n::Node) friend_str = join(map((x) -> string(x.data), collect(n.friend)), ", ") println(io, "data: {", n.data, "}, friend: {", friend_str, "}") end
グラフ上のノードにおいて、queryに対してk近傍のデータを検索する knn_search を実装します。
function knn_search(nodes::Vector{Node}, q, m::Int, k::Int) visited_set = Set() canditates = PriorityQueue() result = PriorityQueue() for _ in 1:m if length(visited_set) == length(nodes) break end tmp_result = Vector{Node}() while true ri = rand(1:length(nodes), 1)[1] node = nodes[ri] if !in(node, visited_set) push!(visited_set, node) enqueue!(canditates, node=>norm(node.data .- q)) push!(tmp_result, node) break end end while true if length(canditates) == 0 break end c = dequeue!(canditates) c_d = norm(c.data .- q) result_collect = collect(result) if length(result_collect) >= k n = result_collect[k] if c_d >= n[2] break end end for node in c.friend if !in(node, visited_set) push!(visited_set, node) enqueue!(canditates, node=>norm(node.data .- q)) push!(tmp_result, node) end end end for node in tmp_result enqueue!(result, node=>norm(node.data .- q)) end end result_collect = collect(result)[1:k] result_v = Vector() for r in result_collect push!(result_v, r[1]) end return result_v end
新しいノードの追加は knn_search を使ってk近傍のノードを接続します。複数のノード群からnswを構築する nsw_build も作成しておきます。
初期の knn_search によって長距離のリンクが作られることがポイントです。
function nearest_neighbor_insert(nodes, new_node, f, w) neighbors = knn_search(nodes, new_node.data, w, f) for node in neighbors push!(node.friend, new_node) push!(new_node.friend, node) end end function nsw_build(nodes, f, w) for new_node in nodes nearest_neighbor_insert(nodes, new_node, f, w) end end
queryに対する最近傍探索は隣接ノードから最も近いノードをgreedyに探索していきます。
function greedy_searh(nodes, q) ri = rand(1:length(nodes), 1)[1] near_node = nodes[ri] min_d = norm(near_node.data .- q) while true break_flg = true for node in near_node.friend d = norm(node.data - q) if d < min_d min_d = d near_node = node break_flg = false end end if break_flg break end end return near_node end
以上で実装は終わりです。 試しに以下のように2次元の範囲[0, 1)の乱数データ1000個に対してテストしてみます。
Random.seed!(1234) n = 1000 # number of node dim = 2 # dimension nodes = [Node(rand(dim), Set()) for i in 1:1000] nsw_build(nodes, 10, 10) q = rand(dim) println("query: ", q) res = greedy_searh(nodes, q) println("result: ", res.data) l2 = norm(res.data .- q) println("l2 distance: ", l2)
query: [0.10217918147914129, 0.6093148458481783] result: [0.09006444691972337, 0.6142456375838046] l2 distance: 0.013079736258246004
queryに対して近傍のデータが検索できていることが分かります。
gist
こちらにコードをおいておきます
参考
- Malkov, Yury, et al. "Approximate nearest neighbor algorithm based on navigable small world graphs." Information Systems 45 (2014): 61-68.
- Malkov, Yury A., and Dmitry A. Yashunin. "Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs." IEEE transactions on pattern analysis and machine intelligence (2018).
スチューデントのt分布の最尤推定
スチューデントのt分布は外れ値のあるデータに対してもロバストな推定を可能とする分布として知られている。忘備録としてこの記事では、そのt分布の最尤推定をする。
スチューデントのt分布
一次元のt分布は、パラメータを用いて次のような確率密度関数で表すことができる。

EMアルゴリズム
最尤推定には、EMアルゴリズムを用いる。をデータ、
を潜在変数、
をパラメータとする。
次式で尤度関数と対数尤度関数を示す。


Eステップ
の事後分布を計算する。

の事後分布による
の期待値は以下のようになる。


Mステップ
対数尤度関数の期待値を最大化するように、それぞれのパラメータを更新する。




ただし、パラメータに関しては、上の式のように解析解が得られないのでニュートン法による数値解析によってパラメータを更新する。


このようにEステップ、Mステップを繰り返すことによって尤度関数を最大化させて最尤推定をする。
実装
juliaを用いて実装をする。外れ値による影響を正規分布と比較するために、から10のデータのサンプルに
から生起されるデータを1つ加えたデータセットでそれぞれを最尤推定して比較する。
using Plots using StatsPlots using Random using Distributions using SpecialFunctions using Statistics using StatsBase using Optim using ReverseDiff: gradient Random.seed!(1234) function e_eta(x, nu, lambda_, mu) return (nu + 1)/(nu + lambda_ * (x - mu)^2) end function e_etas(X, nu, lambda_, mu) return [ e_eta(x, nu, lambda_, mu) for x in X] end function e_log_eta(x, nu, lambda_, mu) return digamma((nu + 1.0)/2.0) - log((nu + lambda_ * (x - mu)^2)/2.0) end function e_log_etas(X, nu, lambda_, mu) return [ e_log_eta(x, nu, lambda_, mu) for x in X] end function fit_t(X) n = length(X) # init mu = median(X) lambda_ = iqr(X)/2.0 nu = 1.0 for i in 1:1000 # E step e_etas_ = e_etas(X, nu, lambda_, mu) e_log_etas_ = e_log_etas(X, nu[1], lambda_, mu) # M step # mu mu = (X' * e_etas_) / sum(e_etas_) # lambda_ lambda_ = 1.0 / ( (((X .- mu).^2)' * e_etas_) / n) # nu function f(nu) return digamma(nu[1]/2.0) - log(nu[1]/2.0) - (1.0 + sum(e_log_etas_)/n - sum(e_etas_)/n) end for j in 1:1000 tmp = nu - f([nu])/gradient(f, [nu])[1] if !isnan(tmp) nu = max(tmp, 1e-6) if abs(f([nu])) < 1e-6 break end else break end end end return mu, lambda_, nu end d = Normal(0.0, 1.0) noise_d = Normal(100.0, 1.0) data = rand(d, 10) outlier = rand(noise_d, 1) X = vcat(data, outlier) mu, lambda_, nu = fit_t(X) scatter(data, zeros(length(data)), label="data") scatter!(outlier, zeros(length(outlier)), label="outlier") plot!(fit_mle(Normal, X), label="Normal") Xs = Array(range(-100, 120, step=0.1)) function t_pdf(x, mu, lamda_, nu) return gamma((nu+1)/2)./gamma(nu/2).*sqrt(lambda_/(pi*nu)).*(1 .+ lambda_*(x .- mu).^2/nu).^(-(nu+1)/2) end Ys = t_pdf(Xs, mu, lambda_, nu) plot!(Xs, Ys.*0.035, label="Student t Distribution", title="MLE of the Student t distribution using EM Algorithm")

上記の結果のように正規分布は、外れ値に引っ張られた推定をしていることが分かる。一方、t分布は外れ値に対してロバストに推定可能であることが分かる。
notebook
参考
TerraformでFizzBuzz
ネタです。
Terraformとは

AWS、GCP、Azureなどのクラウドやサービスのプロビジョニングと管理を行うInfrastructure as Code(IaC)ツールです。 今回はこのTerraformを使ってFizzBuzzを書いていきます。
Terraformの環境構築
0.13.0-beta1 と 0.12.1 の2つの環境を用意します。理由は後述します。
wget https://releases.hashicorp.com/terraform/0.13.0-beta1/terraform_0.13.0-beta1_linux_amd64.zip unzip terraform_0.13.0-beta1_linux_amd64.zip mv terraform terraform_0.13 wget https://releases.hashicorp.com/terraform/0.12.1/terraform_0.12.1_linux_amd64.zip unzip terraform_0.12.1_linux_amd64.zip mv terraform terraform_0.12.1
rangeを使った方法(IaC感がない)
TerraformにはいくつかのBuilt-in Functionsがあり、中にはCollectionの関数でrangeがあります。
さらには三項演算子もあり、for文もあるので以下のように簡単に書くことができます。
main.tf
output "out" { value = [ for i in range(1, 101): i % 15 == 0 ? "FizzBuzz" : i % 5 == 0 ? "Buzz" : i % 3 == 0 ? "Fizz" : i ] }
これを 0.13.0-beta1 で実行すると以下のようにFuzzBuzzが実装されていることが分かると思います。
❯ ./terraform_0.13 apply -auto-approve Apply complete! Resources: 0 added, 0 changed, 0 destroyed. Outputs: out = [ "1", "2", "Fizz", "4", "Buzz", "Fizz", "7", "8", "Fizz", "Buzz", "11", "Fizz", "13", "14", "FizzBuzz", ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "Buzz", "Fizz", "97", "98", "Fizz", "Buzz", ]
しかし、このコードは 0.12.1 では実行できません。
❯ ./terraform_0.12.1 apply -auto-approve Error: Error locking state: Error acquiring the state lock: state snapshot was created by Terraform v0.13.0, which is newer than current v0.12.1; upgrade to Terraform v0.13.0 or greater to work with this state Terraform acquires a state lock to protect the state from being written by multiple users at the same time. Please resolve the issue above and try again. For most commands, you can disable locking with the "-lock=false" flag, but this is not recommended.
なぜなら range 関数は 0.12.2 から追加された関数だからです。
何よりインフラを構築するツールなのに何も構築していないのでIaC感がないのが気になります。
Release v0.12.2 · hashicorp/terraform · GitHub
countを使った方法
そこでcountというパラメータを使用します。これは同じリソースを複数作成する際に用いるパラメータです。例えば100個同じリソースを作りたい場合はcount を100に設定します。 また、count.index を使うことでそれぞれのリソースのindexを取得できるので、1から100までの連番の生成が可能となります。以上のものを使って0.12.2 でも動くようにするのとIaC感があるコードになりそうですね!!
main.tf
今回はproviderにdockerを使ってdockerのリソースを複数作成して実装していきます。 dockerのコンテナを複数作成するように実装していきます。
terraform { required_providers { docker = { source = "terraform-providers/docker" } } required_version = ">= 0.13" } provider "docker" { host = "unix:///var/run/docker.sock" } resource "docker_container" "hello" { count = 15 image = docker_image.hello.latest name = "name-${count.index}" labels { label = "label-${count.index}" value = (count.index + 1) % 15 == 0 ? "FizzBuzz" : (count.index + 1) % 5 == 0 ? "Buzz" : (count.index + 1) % 3 == 0 ? "Fizz" : (count.index + 1) } } resource "docker_image" "hello" { name = "hello-world:latest" } output "out" { value = [for o in docker_container.hello : o.labels.*.value] }
とりあえず1から15までを実行した結果が以下のようになります。
❯ terraform apply -auto-approve ❯ terraform output out = [ [ "1", ], [ "2", ], [ "Fizz", ], [ "4", ], [ "Buzz", ], [ "Fizz", ], [ "7", ], [ "8", ], [ "Fizz", ], [ "Buzz", ], [ "11", ], [ "Fizz", ], [ "13", ], [ "14", ], [ "FizzBuzz", ], ]
一見成功してそうに見えますが、上記の count を100にして1から100で実行すると以下のようにコンテナが建てられず、Errorが出てしまいFizzBuzzが実装できないです。
running状態にならなかった場合にはnullが入ってしまいます。
❯ terraform apply -auto-approve ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Error: Container 33111f01371fcff7a1de675ffb77523006fda97f869665e61d3e9dc5c3fc19d0 failed to be in running state on main.tf line 14, in resource "docker_container" "hello": 14: resource "docker_container" "hello" { ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ❯ terraform output out = [ null, null, null, null, null, [ "Fizz", ], null, null, null, null, [ "11", ], null, null, null, null, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ null, null, [ "92", ], null, null, null, null, [ "97", ], ]
main.tf
回避する策としてdockerのvolumeを複数作成するように変更します。
terraform { required_providers { docker = { source = "terraform-providers/docker" } } required_version = ">= 0.13" } provider "docker" { host = "unix:///var/run/docker.sock" } resource "docker_volume" "volume" { count = 100 name = "name-${count.index}" labels { label = "label-${count.index}" value = (count.index + 1) % 15 == 0 ? "FizzBuzz" : (count.index + 1) % 5 == 0 ? "Buzz" : (count.index + 1) % 3 == 0 ? "Fizz" : (count.index + 1) } } output "out" { value = [for o in docker_volume.volume : o.labels.*.value] }
❯ terraform apply -auto-approve ❯ terraform output out = [ [ "1", ], [ "2", ], [ "Fizz", ], [ "4", ], [ "Buzz", ], [ "Fizz", ], [ "7", ], [ "8", ], [ "Fizz", ], [ "Buzz", ], [ "11", ], [ "Fizz", ], [ "13", ], [ "14", ], [ "FizzBuzz", ], ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ [ "91", ], [ "92", ], [ "Fizz", ], [ "94", ], [ "Buzz", ], [ "Fizz", ], [ "97", ], [ "98", ], [ "Fizz", ], [ "Buzz", ], ]
うまくいきましたね!!これで古い環境でもFizzBuzzが実装できるようになりました!!
このコードをクラウドの高いGPUインスタンスで実行してみたいので誰か僕に寄付してください(やりません)。
Repository
効率的フロンティアの解析解
現代ポートフォリオ理論の効率的フロンティアの解析解について調べたことをまとめました。
卵は一つのカゴに盛るな
ファイナンスの世界では、先人たちの経験をもとにした「卵は一つのカゴに盛るな」という格言があります。 これは一つのカゴに全ての卵を盛ると落としたときに全ての卵が割れてしまいますが、複数のカゴに分けて盛ると全ての卵が割れる事態を回避できることを示したものになります。 このようなリスクを最小化する分散投資が重要であることは昔から経験的に知られていました。
現代ポートフォリオ理論とは?
現代ポートフォリオ理論とは、リスクのある投資する場合のポートフォリオの配分をどのように合理的に決定すべきかを示した理論です。 この理論では、投資家は同じリターンが見込まれるのであればリスクを回避するという仮定をおいています。 これはポートフォリオの投資収益率の平均・分散にのみを考慮して、投資収益率の分散(リスク)を最小化することを意味します。 分散(リスク)を最小化するためには「卵は一つのカゴに盛るな」という先人の知恵を活かします。
卵を複数のカゴに分けるようにそれぞれのポートフォリオの配分をとします。
それぞれ投資収益率の平均
・分散
は次のように示されます。
ポートフォリオ数は
、ポートフォリオの共分散行列の要素を
とします
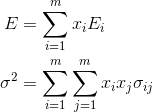
この式からポートフォリオの配分を変えることによって、投資収益率の分散(リスク)をコントロールすることが可能であることが分かります。
効率的フロンティアの解析解
分散を最小化した場合の、リスク・リターン平面における曲線は最小分散フロンティアと呼ばれており、その中でリターンが高いものを効率的フロンティアと言います。 その解析解を求めます。 以下のように、等式制約がある最適化問題として定式化します。
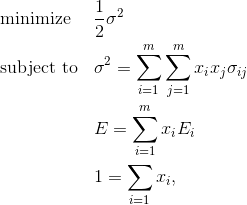
この問題は、ラグランジュの未定乗数法を使用することで解析解を求めることが可能となります。 ラグランジュ関数は以下のようになります。
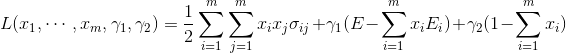
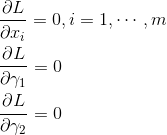
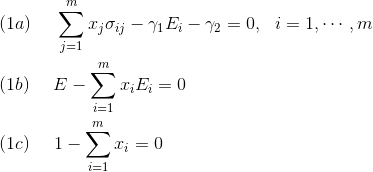
式は
に対して線形なので共分散行列の逆行列の要素
を使って以下のように書き換えることが可能です。
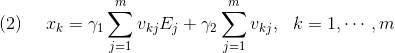
式に
をかけて
について合計すると以下のようになります。
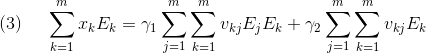
さらに、式を
について合計すると以下のようになります。
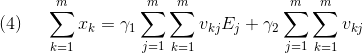
それぞれ を以下のように定義すると式
から
についての線形式が導出されます。
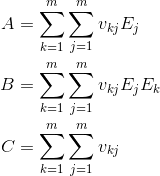
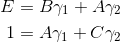
とすると、
は以下のように解けます。
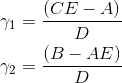
次に式 に
をかけて
について合計したものが次のようになります。
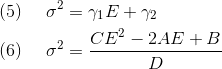
式(6)が最小分散フロンティアです。 このようにして解析解を得ることができました。 次に、テストデータを使って効率的フロンティアをプロットしていきます。
実装
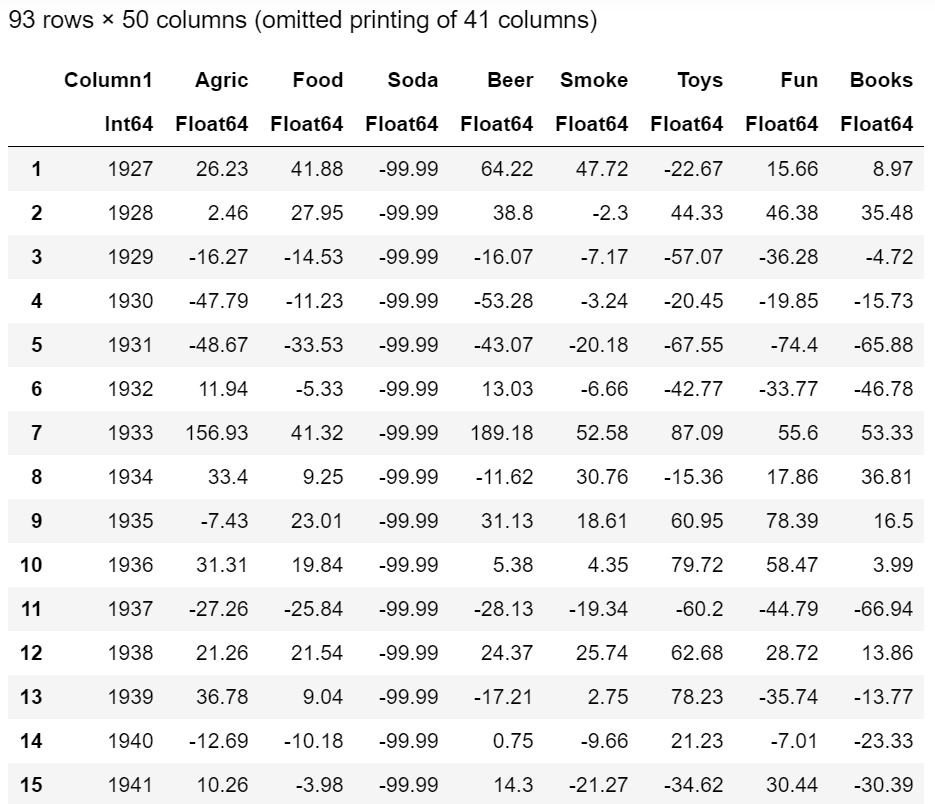
以下は、Juliaで実装したコードです。
using Plots using Statistics using DataFrames using CSV using LinearAlgebra open("./49_Industry_Portfolios.CSV", "r") do f global df csv = join(readlines(f)[2268:2361], '\n') df = CSV.read(IOBuffer(csv)) end # preprocessing inds = describe(df).min .> -99 # remove missing value inds[1] = 0 # remove year inds = inds .* range(1; stop=length(inds)) filter!(x -> x > 0, inds) df_sub = df[:, inds] mat = convert(Matrix, df_sub) E = mean(mat; dims=1) v = inv(cov(mat)) n = size(mat)[2] A = 0.0 for i in 1:n for j in 1:n A += v[i,j]E[j] end end B = 0.0 for i in 1:n for j in 1:n B += v[i,j]E[i]E[j] end end C = 0.0 for i in 1:n for j in 1:n C += v[i,j] end end D = B*C - A^2 function sigma(E) sqrt((C * E^2 - 2A * E + B)/D) end # portfolio scatter(sqrt.(diag(cov(mat))), E', label="portforio") # global minimum variance portfolio y = A/C x = sigma(y) scatter!([x], [y], label="global minimum variance portfolio") # effirencent frontier E_min = A/C E_max = max(E...) ys = range(E_min; stop=E_max, length=1000) xs = [sigma(y) for y in ys] plot!(xs, ys, label="efficient frontier") # minimum variance frontier E_min = 2 * A/C - max(E...) E_max= A/C ys = range(E_min; stop=E_max, length=1000) xs = [sigma(y) for y in ys] plot!(xs, ys, linestyle=:dash, xlabel="risk", ylabel="return", label="", title="Modern portfolio theory")
結果
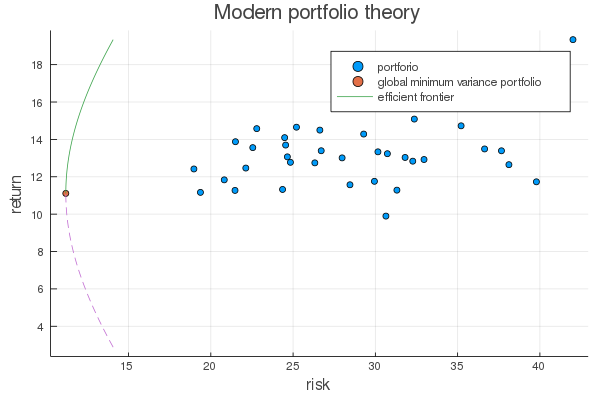
それぞれのポートフォリオが青い点、効率的フロンティア(efficient frontier)は緑の線、分散が最も小さくなる点である最小分散フロンティア(global minimum variance portfolio)はオレンジ色で示されています。 既存のポートフォリオよりリスクが少なくなるような曲線が描かれていることが分かります。 このようにポートフォリオの配分によってリスクを最小化してより良い資産運用をすることが可能となります。
notebook
https://nbviewer.jupyter.org/github/suzusuzu/blog/blob/master/finance/EfficientFrontier.ipynb
参考
- Markowitz, Harry. “Portfolio Selection.” The Journal of Finance, vol. 7, no. 1, 1952, pp. 77–91., doi:10.2307/2975974. Accessed 14 2020.
- Merton, Robert C. "An analytic derivation of the efficient portfolio frontier." Journal of financial and quantitative analysis 7.4 (1972): 1851-1872.
- ウォール街のランダムウォーカー
- Kenneth R. French - Data Library
AV1で採用されているChroma from Luma Prediction (CfL)を使ってイントラ予測
Chroma from Luma Prediction (CfL) はAlliance for Open Mediaが開発したオープンかつロイヤリティフリーな動画圧縮コーデックAV1などで採用されているイントラ予測手法です。イントラ予測というのは動画圧縮で他のフレームを参照しないフレーム符号化のことを言います。今回は、Juliaを用いてその効果を検証していきます。
Chroma(彩度)とLuma(輝度)の関係
CfLはLumaからChromaを推定する手法です。これにより保持すべきデータ容量が削減できます。ここでは、レナの画像を使ってChromaとLumaの関係を可視化します。
まず必要なパッケージを使ってレナの画像を準備します。
using Images, ImageView, TestImages using Plots lena = testimage("lena_color_256") plot(lena)

次にYCbCr色空間に変換します。
lena = YCbCr.(lena) lena_arr = channelview(lena) p_y = heatmap(reverse(lena_arr[1,:,:], dims=1), title="Y(Luma)", color=:grays) p_cb = heatmap(reverse(lena_arr[2,:,:], dims=1), title="Cb", color=:grays) p_cr = heatmap(reverse(lena_arr[3,:,:], dims=1), title="Cr", color=:grays) plot(p_y, p_cb, p_cr, layout=(1, 3), size=(1200, 300), fmt=:png)

左上の32x32のタイル上における、ビットごとのそれぞれChromaとLumaの関係を見ます。横軸にLuma、縦軸にChromaの散布図を作成します。
bs = 32 # block size s = 1 e = s + bs - 1 plot(lena[s:e,s:e], fmt=:png) x_min = minimum(lena_arr[1,s:e,s:e]) x_max = maximum(lena_arr[1,s:e,s:e]) # Cb x = vec(lena_arr[1,s:e,s:e]) y = vec(lena_arr[2,s:e,s:e]) scatter(x, y, label="Cb", xlabel="Luma", ylabel="Chroma") cb_a = (bs*bs*sum(x.*y) - sum(x)*sum(y)) / (sum(bs*bs*(x.^2)) - sum(x)^2) cb_b = (sum(y) - cb_a * sum(x)) / (bs*bs) x = range(x_min, x_max, length=1000) y = cb_a .* x .+ cb_b plot!(x, y, label="Cb prediction") # Cr x = vec(lena_arr[1,s:e,s:e]) y = vec(lena_arr[3,s:e,s:e]) scatter!(x, y, label="Cr") cr_a = (bs*bs*sum(x.*y) - sum(x)*sum(y)) / (sum(bs*bs*(x.^2)) - sum(x)^2) cr_b = (sum(y) - cr_a * sum(x)) / (bs*bs) x = range(x_min, x_max, length=1000) y = cr_a .* x .+ cr_b plot!(x, y, label="Cr prediction", fmt=:png)


上記の結果から、ChromaのそれぞれのCr, CbはLumaに対してのある程度線形な関係にあることが分かりました。つまりCr, Cbはそれぞれ傾きと切片が分かっているならLumaからある程度推定可能ということです。この関係を用いてCfLを実装します。
Chroma from Luma Prediction (CfL)
先程の例でChromaとLumaの関係が分かっているのであとは定式化してみましょう。
Predicting Chroma from Luma in AV1 から式を引用するとCfLは以下のようなパラメータの線形モデルを使って推定します。
はChroma, Lumaです。

パラメータは次のように最小二乗法で求めます。

最後に、8, 16, 32のブロックサイズごとにCfLをした画像とオリジナル画像を比較してみましょう。
function cfl(img_arr, bs=8) nc, h, w = size(img_arr) img_arr_est = zeros((nc, h, w)) for i in 1:Int(h/bs) si = (i-1)*bs + 1 ei = i*bs for j in 1:Int(w/bs) sj = (j-1)*bs + 1 ej = j*bs img_arr_tmp = img_arr[:, si:ei, sj:ej] # Cb x = vec(img_arr_tmp[1, :, :]) y = vec(img_arr_tmp[2, :, :]) cb_a = (bs*bs*sum(x.*y) - sum(x)*sum(y)) / (sum(bs*bs*(x.^2)) - sum(x)^2) cb_b = (sum(y) - cb_a * sum(x)) / (bs*bs) # Cr x = vec(img_arr_tmp[1, :, :]) y = vec(img_arr_tmp[3, :, :]) cr_a = (bs*bs*sum(x.*y) - sum(x)*sum(y)) / (sum(bs*bs*(x.^2)) - sum(x)^2) cr_b = (sum(y) - cr_a * sum(x)) / (bs*bs) x = img_arr_tmp[1, :, :] cb_est = cb_a .* x .+ cb_b cr_est = cr_a .* x .+ cr_b img_arr_est_tmp = zeros((3, bs, bs)) img_arr_est_tmp[1,:,:] .= x img_arr_est_tmp[2,:,:] .= cb_est img_arr_est_tmp[3,:,:] .= cr_est img_arr_est[:, si:ei, sj:ej] .= img_arr_est_tmp end end img_arr_est end p_org = plot(colorview(YCbCr, lena_arr), title="origin") p8 = plot(colorview(YCbCr, cfl(lena_arr, 8)), title="CfL(block size 8)") p16 = plot(colorview(YCbCr, cfl(lena_arr, 16)), title="CfL(block size 16)") p32 = plot(colorview(YCbCr, cfl(lena_arr, 32)), title="CfL(block size 32)") plot(p_org, p8, p16, p32, layout = (1, 4), size = (1200, 300), fmt=:png)

上記の結果からオリジナル画像に対して、CfLでかなりきれいに推定できることが分かりました。 AV1では、上記のような基本的なCfLが用いられているわけではないのですが原理は同じです。 さらに今後の取り組みとして非線形モデルを使って推定するなども考えられているらしいです。

notebook
参考
RustのHashMapの再現性を確保する
Rustの標準のHashMapのハッシュアルゴリズムでは再現性を確保することができないので,別のハッシュアルゴリズムを使って再現性を確保する方法をメモしておく.これはHashSetの場合も同様に再現性を確保することができます.
HashMapのランダム性
By default, HashMap uses a hashing algorithm selected to provide resistance against HashDoS attacks. The algorithm is randomly seeded, and a reasonable best-effort is made to generate this seed from a high quality, secure source of randomness provided by the host without blocking the program.
上記の引用のように,標準のHashMapのハッシュアルゴリズムではHashDoS攻撃を防ぐためにランダム性があり,同じコードでも再現不可能となる場合があります.
再現不可能なコード
例えば以下のようなコードは実行ごとに結果が異なります.
use std::collections::HashMap; fn main() { let mut map = HashMap::new(); for i in 0..10 { map.insert(i, i); } let _ = map.iter().map(|x| print!("{:?},", x)).collect::<Vec<_>>(); println!(""); }
実行1
(1, 1),(7, 7),(8, 8),(6, 6),(3, 3),(4, 4),(0, 0),(9, 9),(2, 2),(5, 5),
実行2
(0, 0),(3, 3),(5, 5),(6, 6),(2, 2),(4, 4),(7, 7),(8, 8),(9, 9),(1, 1),
rust-fnv
fnvはkeyのサイズが小さい場合に効率的に動作するハッシュアルゴリズムです. このライブラリには,標準のHashMapをfnvハッシュアルゴリズムに代替してエイリアスされたものがあります.今回はこれを使用して再現性を確保します.
再現可能なコード
use fnv::FnvHashMap; fn main() { let mut map = FnvHashMap::default(); for i in 0..10 { map.insert(i, i); } let _ = map.iter().map(|x| print!("{:?},", x)).collect::<Vec<_>>(); println!(""); }
実行1
(5, 5),(4, 4),(7, 7),(6, 6),(1, 1),(0, 0),(3, 3),(2, 2),(9, 9),(8, 8),
実行2
(5, 5),(4, 4),(7, 7),(6, 6),(1, 1),(0, 0),(3, 3),(2, 2),(9, 9),(8, 8),